Simple Multigrid Examples

Simple Multigrid Examples#

Known Solution#

A basic multigrid test is run as (using a path relative to the root of the pyro2 repository):

./pyro/multigrid/examples/mg_test_simple.py

The mg_test_simple.py script solves a Poisson equation with a known analytic solution. This particular example comes from the text A Multigrid Tutorial, 2nd Ed., by Briggs. The example is:

\[u_{xx} + u_{yy} = -2 \left [(1-6x^2)y^2(1-y^2) + (1-6y^2)x^2(1-x^2)\right ]\]

on \([0,1] \times [0,1]\) with \(u = 0\) on the boundary.

The solution to this is shown below.

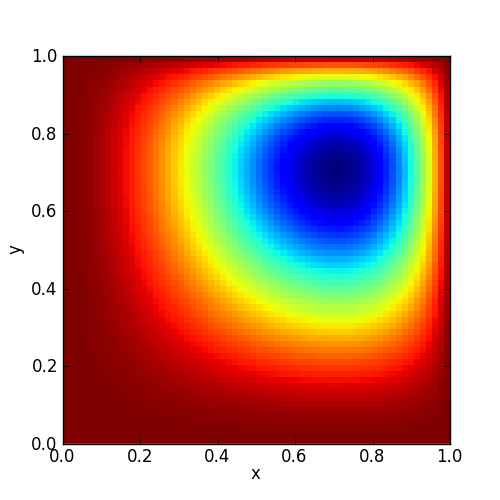
_images/mg_test.png

Since this has a known analytic solution:

\[u(x,y) = (x^2 - x^4)(y^4 - y^2)\]

We can assess the convergence of our solver by running at a variety of resolutions and computing the norm of the error with respect to the analytic solution. This is shown below:

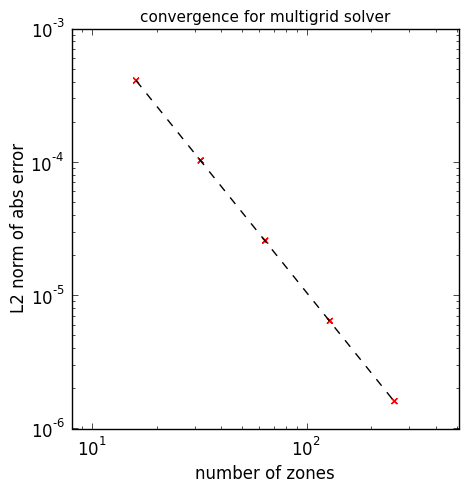
_images/mg_converge.png

The dotted line is 2nd order convergence, which we match perfectly.

The movie below shows the smoothing at each level to realize this solution:


You can run this example locally by running the mg_vis.py script:

./pyro/multigrid/examples/mg_vis.py

Projection#

Another example uses multigrid to extract the divergence free part of a velocity field. The script to run this is project_periodic.py. This is run as:

./pyro/multigrid/examples/project_periodic.py

Given a vector field, \(U\), we can decompose it into a divergence free part, \(U_d\), and the gradient of a scalar, \(\phi\):

\[U = U_d + \nabla \phi\]

We can project out the divergence free part by taking the divergence, leading to an elliptic equation:

\[\nabla^2 \phi = \nabla \cdot U\]

The project-periodic.py script starts with a divergence free velocity field, adds to it the gradient of a scalar, and then projects it to recover the divergence free part. The error can found by comparing the original velocity field to the recovered field. The results are shown below:

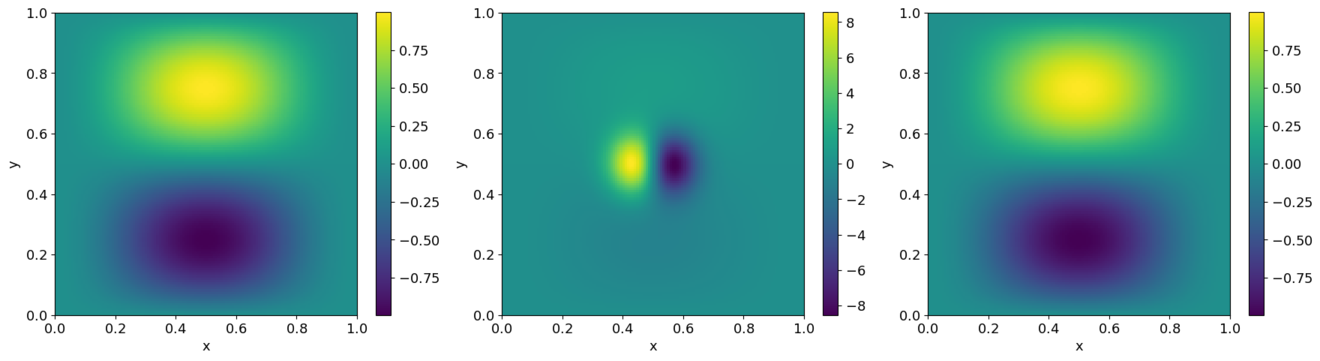
_images/project.png

Left is the original u velocity, middle is the modified field after adding the gradient of the scalar, and right is the recovered field.

Exercises#

Explorations#

  • Try doing just smoothing, no multigrid. Show that it still converges second order if you use enough iterations, but that the amount of time needed to get a solution is much greater.

Extensions#

  • Add a different bottom solver to the multigrid algorithm

  • Make the multigrid solver work for non-square domains

  • Implement the full-multigrid algorithm instead of just V-cycles