Constant-Coefficient Poisson Equation#
We want to solve
on
with homogeneous Dirichlet boundary conditions (this example comes from A Multigrid Tutorial).
This has the analytic solution
[1]:
import numpy as np
import matplotlib.pyplot as plt
Setting up the solver#
We start by setting up a multigrid object—this needs to know the number of zones our problem is defined on
[2]:
import pyro.multigrid.MG as MG
[3]:
nx = ny = 256
mg = MG.CellCenterMG2d(nx, ny,
xl_BC_type="dirichlet", xr_BC_type="dirichlet",
yl_BC_type="dirichlet", yr_BC_type="dirichlet", verbose=1)
cc data: nx = 2, ny = 2, ng = 1
nvars = 3
variables:
v: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
f: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
r: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
cc data: nx = 4, ny = 4, ng = 1
nvars = 3
variables:
v: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
f: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
r: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
cc data: nx = 8, ny = 8, ng = 1
nvars = 3
variables:
v: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
f: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
r: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
cc data: nx = 16, ny = 16, ng = 1
nvars = 3
variables:
v: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
f: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
r: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
cc data: nx = 32, ny = 32, ng = 1
nvars = 3
variables:
v: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
f: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
r: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
cc data: nx = 64, ny = 64, ng = 1
nvars = 3
variables:
v: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
f: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
r: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
cc data: nx = 128, ny = 128, ng = 1
nvars = 3
variables:
v: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
f: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
r: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
cc data: nx = 256, ny = 256, ng = 1
nvars = 3
variables:
v: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
f: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
r: min: 0.0000000000 max: 0.0000000000
BCs: -x: dirichlet +x: dirichlet -y: dirichlet +y: dirichlet
Next, we initialize the RHS. To make life easier, the CellCenterMG2d object has the coordinates of the solution grid (including ghost cells) as mg.x2d and mg.y2d (these are two-dimensional arrays).
[4]:
def rhs(x, y):
return -2.0 * ((1.0 - 6.0 * x**2) * y**2 * (1.0 - y**2) +
(1.0 - 6.0 * y**2) * x**2 * (1.0 - x**2))
[5]:
mg.init_RHS(rhs(mg.x2d, mg.y2d))
Source norm = 1.097515813669473
The last setup step is to initialize the solution–this is the starting point for the solve. Usually we just want to start with all zeros, so we use the init_zeros() method
[6]:
mg.init_zeros()
Performing the solve#
We can now solve—there are actually two different techniques we can do here. We can just do pure smoothing on the solution grid using mg.smooth(mg.nlevels-1, N), where N is the number of smoothing iterations. To get the solution N will need to be large and this will take a long time.
Multigrid accelerates the smoothing. We can do a V-cycle multigrid solution using mg.solve()
[7]:
mg.solve()
source norm = 1.097515813669473
<<< beginning V-cycle (cycle 1) >>>
level = 7, nx = 256, residual change: 1.09752 → 1.50231
level = 6, nx = 128, residual change: 1.06162 → 1.43215
level = 5, nx = 64, residual change: 1.01137 → 1.28187
level = 4, nx = 32, residual change: 0.903531 → 0.960758
level = 3, nx = 16, residual change: 0.673611 → 0.443977
level = 2, nx = 8, residual change: 0.307211 → 0.0727216
level = 1, nx = 4, residual change: 0.0484181 → 3.96107e-05
bottom solve
level = 1, nx = 4, residual change: 3.92501e-05 → 3.92501e-05
level = 2, nx = 8, residual change: 0.0701013 → 0.0701013
level = 3, nx = 16, residual change: 0.430738 → 0.430738
level = 4, nx = 32, residual change: 0.911086 → 0.911086
level = 5, nx = 64, residual change: 1.19454 → 1.19454
level = 6, nx = 128, residual change: 1.31346 → 1.31346
level = 7, nx = 256, residual change: 1.36183 → 1.36183
cycle 1: relative err = 0.999999999999964, residual err = 0.02448256984911586
<<< beginning V-cycle (cycle 2) >>>
level = 7, nx = 256, residual change: 0.02687 → 0.0257902
level = 6, nx = 128, residual change: 0.0182181 → 0.0236543
level = 5, nx = 64, residual change: 0.0166908 → 0.0197734
level = 4, nx = 32, residual change: 0.0139226 → 0.0135776
level = 3, nx = 16, residual change: 0.00951831 → 0.00611516
level = 2, nx = 8, residual change: 0.00424463 → 0.00106741
level = 1, nx = 4, residual change: 0.000710814 → 5.81825e-07
bottom solve
level = 1, nx = 4, residual change: 5.76528e-07 → 5.76528e-07
level = 2, nx = 8, residual change: 0.00102915 → 0.00102915
level = 3, nx = 16, residual change: 0.00623945 → 0.00623945
level = 4, nx = 32, residual change: 0.0145734 → 0.0145734
level = 5, nx = 64, residual change: 0.0215643 → 0.0215643
level = 6, nx = 128, residual change: 0.0257909 → 0.0257909
level = 7, nx = 256, residual change: 0.0280513 → 0.0280513
cycle 2: relative err = 13.739483825281054, residual err = 0.0004957445615074047
<<< beginning V-cycle (cycle 3) >>>
level = 7, nx = 256, residual change: 0.000544087 → 0.000509584
level = 6, nx = 128, residual change: 0.000359788 → 0.000446485
level = 5, nx = 64, residual change: 0.000314789 → 0.000349254
level = 4, nx = 32, residual change: 0.000245728 → 0.000222329
level = 3, nx = 16, residual change: 0.000155893 → 9.51109e-05
level = 2, nx = 8, residual change: 6.6169e-05 → 1.71101e-05
level = 1, nx = 4, residual change: 1.13952e-05 → 9.33005e-09
bottom solve
level = 1, nx = 4, residual change: 9.24513e-09 → 9.24513e-09
level = 2, nx = 8, residual change: 1.64992e-05 → 1.64992e-05
level = 3, nx = 16, residual change: 0.000100977 → 0.000100977
level = 4, nx = 32, residual change: 0.000257541 → 0.000257541
level = 5, nx = 64, residual change: 0.000411339 → 0.000411339
level = 6, nx = 128, residual change: 0.000523281 → 0.000523281
level = 7, nx = 256, residual change: 0.000594507 → 0.000594507
cycle 3: relative err = 34.347638624909216, residual err = 1.0447352805871284e-05
<<< beginning V-cycle (cycle 4) >>>
level = 7, nx = 256, residual change: 1.14661e-05 → 1.05447e-05
level = 6, nx = 128, residual change: 7.44281e-06 → 8.95505e-06
level = 5, nx = 64, residual change: 6.31131e-06 → 6.73455e-06
level = 4, nx = 32, residual change: 4.73798e-06 → 4.0918e-06
level = 3, nx = 16, residual change: 2.87103e-06 → 1.63196e-06
level = 2, nx = 8, residual change: 1.13722e-06 → 2.96104e-07
level = 1, nx = 4, residual change: 1.97219e-07 → 1.61504e-10
bottom solve
level = 1, nx = 4, residual change: 1.60034e-10 → 1.60034e-10
level = 2, nx = 8, residual change: 2.85569e-07 → 2.85569e-07
level = 3, nx = 16, residual change: 1.78938e-06 → 1.78938e-06
level = 4, nx = 32, residual change: 4.9713e-06 → 4.9713e-06
level = 5, nx = 64, residual change: 8.28164e-06 → 8.28164e-06
level = 6, nx = 128, residual change: 1.08889e-05 → 1.08889e-05
level = 7, nx = 256, residual change: 1.27175e-05 → 1.27175e-05
cycle 4: relative err = 0.17409776671446628, residual err = 2.24555429482631e-07
<<< beginning V-cycle (cycle 5) >>>
level = 7, nx = 256, residual change: 2.46453e-07 → 2.24911e-07
level = 6, nx = 128, residual change: 1.58746e-07 → 1.88625e-07
level = 5, nx = 64, residual change: 1.32945e-07 → 1.39771e-07
level = 4, nx = 32, residual change: 9.83693e-08 → 8.26903e-08
level = 3, nx = 16, residual change: 5.80625e-08 → 3.03473e-08
level = 2, nx = 8, residual change: 2.11691e-08 → 5.46752e-09
level = 1, nx = 4, residual change: 3.64181e-09 → 2.98263e-12
bottom solve
level = 1, nx = 4, residual change: 2.95548e-12 → 2.95548e-12
level = 2, nx = 8, residual change: 5.27361e-09 → 5.27361e-09
level = 3, nx = 16, residual change: 3.4147e-08 → 3.4147e-08
level = 4, nx = 32, residual change: 1.03125e-07 → 1.03125e-07
level = 5, nx = 64, residual change: 1.75853e-07 → 1.75853e-07
level = 6, nx = 128, residual change: 2.33838e-07 → 2.33838e-07
level = 7, nx = 256, residual change: 2.75928e-07 → 2.75928e-07
cycle 5: relative err = 0.005391244339065406, residual err = 4.933769007818501e-09
<<< beginning V-cycle (cycle 6) >>>
level = 7, nx = 256, residual change: 5.41489e-09 → 4.94814e-09
level = 6, nx = 128, residual change: 3.49296e-09 → 4.15445e-09
level = 5, nx = 64, residual change: 2.92888e-09 → 3.07478e-09
level = 4, nx = 32, residual change: 2.16499e-09 → 1.78803e-09
level = 3, nx = 16, residual change: 1.25622e-09 → 6.02198e-10
level = 2, nx = 8, residual change: 4.20281e-10 → 1.06557e-10
level = 1, nx = 4, residual change: 7.09787e-11 → 5.81351e-14
bottom solve
level = 1, nx = 4, residual change: 5.76061e-14 → 5.76061e-14
level = 2, nx = 8, residual change: 1.02789e-10 → 1.02789e-10
level = 3, nx = 16, residual change: 6.91401e-10 → 6.91401e-10
level = 4, nx = 32, residual change: 2.25705e-09 → 2.25705e-09
level = 5, nx = 64, residual change: 3.90897e-09 → 3.90897e-09
level = 6, nx = 128, residual change: 5.19639e-09 → 5.19639e-09
level = 7, nx = 256, residual change: 6.11764e-09 → 6.11764e-09
cycle 6: relative err = 7.514139913291318e-05, residual err = 1.111546863428753e-10
<<< beginning V-cycle (cycle 7) >>>
level = 7, nx = 256, residual change: 1.21994e-10 → 1.12199e-10
level = 6, nx = 128, residual change: 7.92186e-11 → 9.49345e-11
level = 5, nx = 64, residual change: 6.69499e-11 → 7.051e-11
level = 4, nx = 32, residual change: 4.96666e-11 → 4.04509e-11
level = 3, nx = 16, residual change: 2.84315e-11 → 1.25763e-11
level = 2, nx = 8, residual change: 8.77795e-12 → 2.17056e-12
level = 1, nx = 4, residual change: 1.44588e-12 → 1.18429e-15
bottom solve
level = 1, nx = 4, residual change: 1.17352e-15 → 1.17352e-15
level = 2, nx = 8, residual change: 2.09401e-12 → 2.09401e-12
level = 3, nx = 16, residual change: 1.46615e-11 → 1.46615e-11
level = 4, nx = 32, residual change: 5.13071e-11 → 5.13071e-11
level = 5, nx = 64, residual change: 9.00155e-11 → 9.00155e-11
level = 6, nx = 128, residual change: 1.19149e-10 → 1.19149e-10
level = 7, nx = 256, residual change: 1.39072e-10 → 1.39072e-10
cycle 7: relative err = 7.062255558417692e-07, residual err = 2.590386214782638e-12
Plotting the solution#
We can access the solution on the finest grid using get_solution()
[8]:
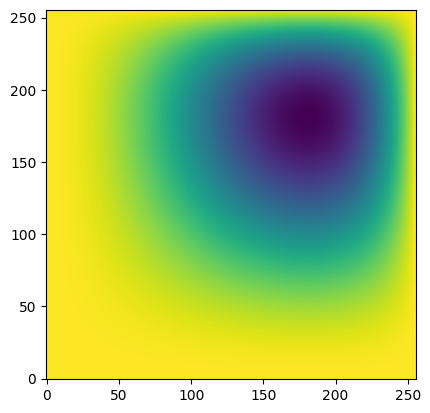
phi = mg.get_solution()
[9]:
fig, ax = plt.subplots()
ax.imshow(np.transpose(phi.v()), origin="lower")
[9]:
<matplotlib.image.AxesImage at 0x7f78d479e900>
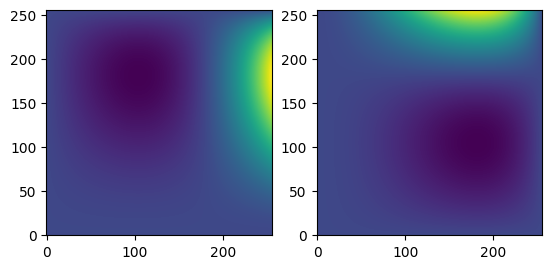
We can also get the gradient of the solution
[10]:
gx, gy = mg.get_solution_gradient()
[11]:
fig = plt.figure()
ax = fig.add_subplot(121)
ax.imshow(np.transpose(gx.v()), origin="lower")
ax = fig.add_subplot(122)
ax.imshow(np.transpose(gy.v()), origin="lower")
[11]:
<matplotlib.image.AxesImage at 0x7f78d4462d50>