Variable Coefficient Poisson#
We want to solve an equation of the form \(\nabla \cdot (\alpha \nabla \phi) = f\)
We’ll do this with periodic boundary conditions. Consider the coefficient \(\alpha\) of the form:
and the source, \(f\):
The solution to this (with periodic BCs) is:
[1]:
import numpy as np
import matplotlib.pyplot as plt
Setting up the solver#
[2]:
import pyro.multigrid.variable_coeff_MG as MG
[3]:
def true(x, y):
return np.sin(2.0*np.pi*x)*np.sin(2.0*np.pi*y)
[4]:
def alpha(x, y):
return 2.0 + np.cos(2.0*np.pi*x)*np.cos(2.0*np.pi*y)
[5]:
def f(x, y):
return -16.0*np.pi**2*(np.cos(2*np.pi*x)*np.cos(2*np.pi*y) + 1) * \
np.sin(2*np.pi*x)*np.sin(2*np.pi*y)
Let’s create a patch to store the coefficient \(\alpha\)
[6]:
from pyro.mesh import patch
import pyro.mesh.boundary as bnd
[7]:
N = 128
g = patch.Grid2d(N, N, ng=1)
d = patch.CellCenterData2d(g)
bc_alpha = bnd.BC(xlb="periodic", xrb="periodic",
ylb="periodic", yrb="periodic")
d.register_var("alpha", bc_alpha)
d.create()
Now we can fill the coefficient
[8]:
a = d.get_var("alpha")
a[:, :] = alpha(g.x2d, g.y2d)
With periodic BCs, solvability requires that \(f\) sum to zero over the domain. Let’s check that.
[9]:
rhs = f(g.x2d, g.y2d)
print(f"rhs sum: {np.sum(rhs[g.ilo:g.ihi+1, g.jlo:g.jhi+1]):20.10g}")
rhs sum: 2.07633187e-12
Now we can create the multigrid object
[10]:
mg = MG.VarCoeffCCMG2d(N, N,
xl_BC_type="periodic", yl_BC_type="periodic",
xr_BC_type="periodic", yr_BC_type="periodic",
coeffs=a, coeffs_bc=bc_alpha,
verbose=1, vis=0, true_function=true)
cc data: nx = 2, ny = 2, ng = 1
nvars = 4
variables:
v: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
f: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
r: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
coeffs: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
cc data: nx = 4, ny = 4, ng = 1
nvars = 4
variables:
v: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
f: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
r: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
coeffs: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
cc data: nx = 8, ny = 8, ng = 1
nvars = 4
variables:
v: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
f: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
r: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
coeffs: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
cc data: nx = 16, ny = 16, ng = 1
nvars = 4
variables:
v: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
f: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
r: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
coeffs: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
cc data: nx = 32, ny = 32, ng = 1
nvars = 4
variables:
v: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
f: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
r: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
coeffs: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
cc data: nx = 64, ny = 64, ng = 1
nvars = 4
variables:
v: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
f: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
r: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
coeffs: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
cc data: nx = 128, ny = 128, ng = 1
nvars = 4
variables:
v: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
f: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
r: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
coeffs: min: 0.0000000000 max: 0.0000000000
BCs: -x: periodic +x: periodic -y: periodic +y: periodic
Initialize the solution to 0
[11]:
mg.init_zeros()
Now initialize the RHS
[12]:
rhs = f(mg.x2d, mg.y2d)
mg.init_RHS(rhs)
Source norm = 81.3868428575047
Solving the system#
[13]:
mg.solve(rtol=1.e-11)
source norm = 81.3868428575047
<<< beginning V-cycle (cycle 1) >>>
level = 6, nx = 128, residual change: 81.3868 → 112.091
level = 5, nx = 64, residual change: 79.2048 → 101.02
level = 4, nx = 32, residual change: 71.2411 → 68.0705
level = 3, nx = 16, residual change: 47.6577 → 14.4578
level = 2, nx = 8, residual change: 9.8448 → 0.0171409
level = 1, nx = 4, residual change: 0.0106141 → 1.69329e-16
bottom solve
level = 1, nx = 4, residual change: 3.07629e-16 → 3.07629e-16
level = 2, nx = 8, residual change: 0.0168243 → 0.0168243
level = 3, nx = 16, residual change: 14.4901 → 14.4901
level = 4, nx = 32, residual change: 69.371 → 69.371
level = 5, nx = 64, residual change: 103.884 → 103.884
level = 6, nx = 128, residual change: 115.511 → 115.511
cycle 1: relative err = 1.0000000000000007, residual err = 0.025573219961900512
<<< beginning V-cycle (cycle 2) >>>
level = 6, nx = 128, residual change: 2.08132 → 2.02861
level = 5, nx = 64, residual change: 1.43441 → 1.83684
level = 4, nx = 32, residual change: 1.29871 → 1.24144
level = 3, nx = 16, residual change: 0.877452 → 0.256041
level = 2, nx = 8, residual change: 0.180588 → 0.000272285
level = 1, nx = 4, residual change: 0.000187447 → 6.55867e-17
bottom solve
level = 1, nx = 4, residual change: 1.19217e-16 → 1.19217e-16
level = 2, nx = 8, residual change: 0.000298554 → 0.000298554
level = 3, nx = 16, residual change: 0.33718 → 0.33718
level = 4, nx = 32, residual change: 1.72809 → 1.72809
level = 5, nx = 64, residual change: 2.60971 → 2.60971
level = 6, nx = 128, residual change: 2.89721 → 2.89721
cycle 2: relative err = 2.1803634390217064, residual err = 0.0006486396426301177
<<< beginning V-cycle (cycle 3) >>>
level = 6, nx = 128, residual change: 0.0527907 → 0.0515129
level = 5, nx = 64, residual change: 0.0364241 → 0.0468113
level = 4, nx = 32, residual change: 0.033097 → 0.0318323
level = 3, nx = 16, residual change: 0.0224975 → 0.00656631
level = 2, nx = 8, residual change: 0.00463131 → 6.95479e-06
level = 1, nx = 4, residual change: 4.7921e-06 → 3.47155e-16
bottom solve
level = 1, nx = 4, residual change: 6.30821e-16 → 6.30821e-16
level = 2, nx = 8, residual change: 7.63309e-06 → 7.63309e-06
level = 3, nx = 16, residual change: 0.00864876 → 0.00864876
level = 4, nx = 32, residual change: 0.0442789 → 0.0442789
level = 5, nx = 64, residual change: 0.0665472 → 0.0665472
level = 6, nx = 128, residual change: 0.0736819 → 0.0736819
cycle 3: relative err = 0.04844393523115633, residual err = 1.659245815001406e-05
<<< beginning V-cycle (cycle 4) >>>
level = 6, nx = 128, residual change: 0.00135041 → 0.00131762
level = 5, nx = 64, residual change: 0.000931668 → 0.00119765
level = 4, nx = 32, residual change: 0.000846751 → 0.000816239
level = 3, nx = 16, residual change: 0.000576837 → 0.000168502
level = 2, nx = 8, residual change: 0.00011884 → 1.78399e-07
level = 1, nx = 4, residual change: 1.22925e-07 → 2.1827e-16
bottom solve
level = 1, nx = 4, residual change: 3.96622e-16 → 3.96622e-16
level = 2, nx = 8, residual change: 1.95801e-07 → 1.95801e-07
level = 3, nx = 16, residual change: 0.000221902 → 0.000221902
level = 4, nx = 32, residual change: 0.0011347 → 0.0011347
level = 5, nx = 64, residual change: 0.00170278 → 0.00170278
level = 6, nx = 128, residual change: 0.00188597 → 0.00188597
cycle 4: relative err = 0.0012759605329324085, residual err = 4.2728946362388976e-07
<<< beginning V-cycle (cycle 5) >>>
level = 6, nx = 128, residual change: 3.47757e-05 → 3.38943e-05
level = 5, nx = 64, residual change: 2.39659e-05 → 3.073e-05
level = 4, nx = 32, residual change: 2.1726e-05 → 2.09217e-05
level = 3, nx = 16, residual change: 1.47845e-05 → 4.32098e-06
level = 2, nx = 8, residual change: 3.04737e-06 → 4.57173e-09
level = 1, nx = 4, residual change: 3.15043e-09 → 4.90471e-17
bottom solve
level = 1, nx = 4, residual change: 8.91242e-17 → 8.91242e-17
level = 2, nx = 8, residual change: 5.01821e-09 → 5.01821e-09
level = 3, nx = 16, residual change: 5.68972e-06 → 5.68972e-06
level = 4, nx = 32, residual change: 2.90707e-05 → 2.90707e-05
level = 5, nx = 64, residual change: 4.36992e-05 → 4.36992e-05
level = 6, nx = 128, residual change: 4.85557e-05 → 4.85557e-05
cycle 5: relative err = 3.301203447716335e-05, residual err = 1.1068868945958364e-08
<<< beginning V-cycle (cycle 6) >>>
level = 6, nx = 128, residual change: 9.0086e-07 → 8.76274e-07
level = 5, nx = 64, residual change: 6.19593e-07 → 7.90474e-07
level = 4, nx = 32, residual change: 5.58852e-07 → 5.36009e-07
level = 3, nx = 16, residual change: 3.78756e-07 → 1.10732e-07
level = 2, nx = 8, residual change: 7.80911e-08 → 1.17095e-10
level = 1, nx = 4, residual change: 8.06977e-11 → 5.69861e-16
bottom solve
level = 1, nx = 4, residual change: 1.0355e-15 → 1.0355e-15
level = 2, nx = 8, residual change: 1.28541e-10 → 1.28541e-10
level = 3, nx = 16, residual change: 1.45795e-07 → 1.45795e-07
level = 4, nx = 32, residual change: 7.4452e-07 → 7.4452e-07
level = 5, nx = 64, residual change: 1.12439e-06 → 1.12439e-06
level = 6, nx = 128, residual change: 1.25658e-06 → 1.25658e-06
cycle 6: relative err = 8.544249588823554e-07, residual err = 2.88200772432267e-10
<<< beginning V-cycle (cycle 7) >>>
level = 6, nx = 128, residual change: 2.34558e-08 → 2.27531e-08
level = 5, nx = 64, residual change: 1.6088e-08 → 2.03781e-08
level = 4, nx = 32, residual change: 1.44068e-08 → 1.37252e-08
level = 3, nx = 16, residual change: 9.69812e-09 → 2.83563e-09
level = 2, nx = 8, residual change: 1.99971e-09 → 2.99732e-12
level = 1, nx = 4, residual change: 2.06576e-12 → 1.74907e-17
bottom solve
level = 1, nx = 4, residual change: 3.17826e-17 → 3.17826e-17
level = 2, nx = 8, residual change: 3.29051e-12 → 3.29051e-12
level = 3, nx = 16, residual change: 3.73325e-09 → 3.73325e-09
level = 4, nx = 32, residual change: 1.90594e-08 → 1.90594e-08
level = 5, nx = 64, residual change: 2.89959e-08 → 2.89959e-08
level = 6, nx = 128, residual change: 3.26638e-08 → 3.26638e-08
cycle 7: relative err = 2.210681933627904e-08, residual err = 7.534885150074738e-12
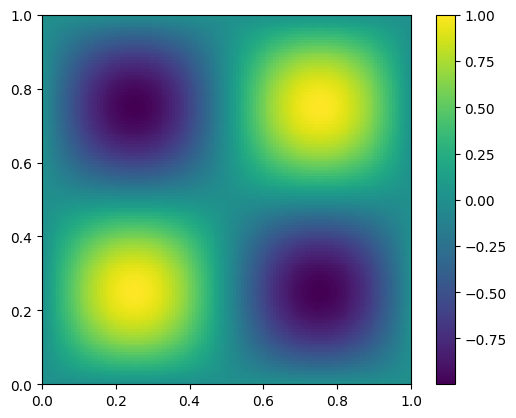
Visualizing the solution#
[14]:
v = mg.get_solution()
[15]:
fig, ax = plt.subplots()
im = ax.imshow(np.transpose(v.v()),
interpolation="nearest", origin="lower",
extent=[mg.xmin, mg.xmax, mg.ymin, mg.ymax])
fig.colorbar(im, ax=ax)
[15]:
<matplotlib.colorbar.Colorbar at 0x7f9a98015160>
Comparing to the exact solution#
[16]:
phi = true(mg.x2d, mg.y2d)
With periodic BCs all around, there is nothing to normalize the solution, so we subtract off the average of \(\phi\) from the MG solution to ensure it is normalized (we’ll do the same with the true solution, just to be sure)
[17]:
e = v - np.sum(v.v()) / N**2 - (phi - np.sum(phi[mg.ilo:mg.ihi+1, mg.jlo:mg.jhi+1]) / N**2)
Now we can look at the norm of the error:
[18]:
error_norm = e.norm()
print(f"error = {error_norm:20.10g}")
error = 9.754984685e-05
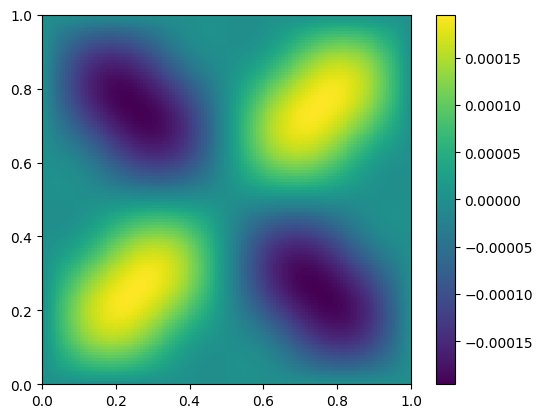
and we can plot the error
[19]:
fig, ax = plt.subplots()
im = ax.imshow(np.transpose(e.v()),
interpolation="nearest", origin="lower",
extent=[mg.xmin, mg.xmax, mg.ymin, mg.ymax])
fig.colorbar(im, ax=ax)
[19]:
<matplotlib.colorbar.Colorbar at 0x7f9a97e69010>