PPM reconstruction

PPMpy provides modules that support a finite-volume discretization on a 1D grid and the ability to reconstruct the cell-average data as parabolas, following the procedure in the original PPM paper (Colella & Woodward 1984).

import numpy as np
import matplotlib.pyplot as plt

FVGrid provides a simple 1D finite-volume grid class. It provides the coordinates for the cells and can create a scratch array defined on the grid. It also knows how to fill ghost cells and compute the norm of the data on the grid. Finally, it includes some methods that allow us to plot the grid.

from ppmpy import FVGrid

An example grid with 4 cells + 3 ghost cells

g = FVGrid(4, 3)

gp = g.draw()

Let’s create data on the grid (including the ghost cells) and visualize the PPM reconstruction.

a = g.scratch_array()
a[:] = [0.3, 1.0, 0.9, 0.8, 0.25, 0.1, 0.5, 0.55, 0.25, 0.1]
a

array([0.3 , 1.  , 0.9 , 0.8 , 0.25, 0.1 , 0.5 , 0.55, 0.25, 0.1 ])

PPMInterpolant manages the PPM reconstruction of the data.

from ppmpy import PPMInterpolant

ppm = PPMInterpolant(g, a)
ppm.construct_parabola()

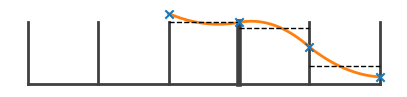
We can now visualize the PPM reconstruction of the data

ppm.draw_parabola(gp)
ppm.mark_cubic(gp)
gp.show_fig()

For comparison, we can look at the unlimited case:

ppm = PPMInterpolant(g, a, limit=False)
ppm.construct_parabola()

gp2 = g.draw()
ppm.draw_parabola(gp2)
ppm.mark_cubic(gp2)

Finally, we can also plot just a portion of the grid:

gp3 = g.draw(hi_index=4)
ppm.draw_parabola(gp3)
ppm.mark_cubic(gp3)