Euler Riemann Problem

To compute the fluxes through the interface, we will need to solve the Riemann problem for the Euler equations. We will formulate it such that we have left and right primitive variable states and we want to find the unique state on the interface:

\[{\bf q}_{i+1/2} = \mathcal{R}({\bf q}_{i+1/2,L}, {\bf q}_{i+1/2,R})\]

Information about the jump across this interface will be carried away from the interface by the 3 hydrodynamic waves (\(u\) and \(u\pm c\)). We can define 4 regions separated by the three waves, which we’ll call \(L\), \(L_\star\), \(R_\star\), and \(R\).

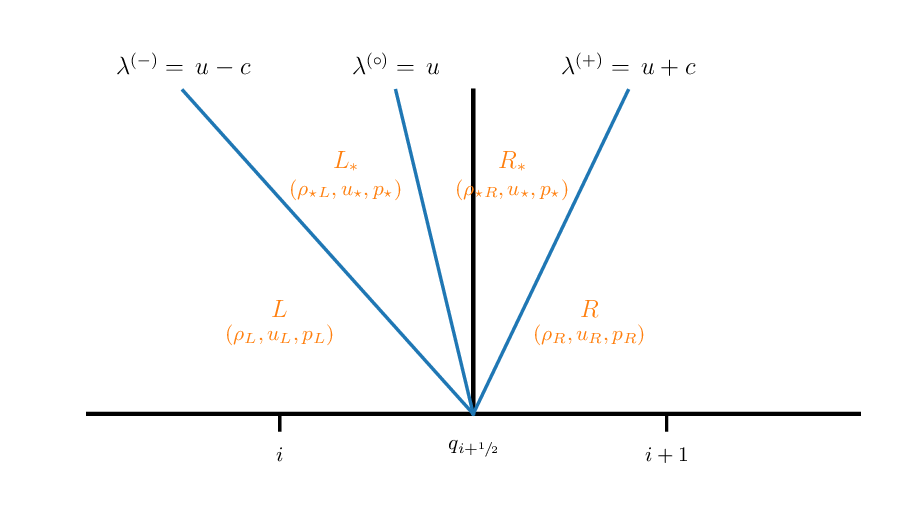
We also know the following about the wave structure:

• The middle wave is always a contact discontinuity. Pressure and velocity are constant across it

• The left and right waves are either a shock or rarefaction

  • Rarefaction:

    • Entropy is constant across the wave

    • Riemann invariants tell us how to connect the solution across the wave to the star region

  • Shock:

    • Must be dissipative—entropy is not conserved

    • Jump conditions tell us how to connect to the star state across the shock

We see that:

• \(L\) and \(R\) are just our original states—since no waves have reached them yet, the state is unchanged.

• The star states are between the left and right state.

  • We know from the eigenvectors that all 3 primitive variables, \((\rho, u, p)\) jump across the left and right state.

  • From the center eigenvector, we know only the density jumps. That means in the star region, the only unknowns are:

    \[u_\star, p_\star, \rho_{\star,L}, \rho_{\star,R}\]

Finding the star state

Our first goal is to find the star state. To do this, we need to know how much each variable changes across each of the three waves. To complicate matters, the left and right waves can be either shocks or rarefactions.
For a gamma-law gas, we can write down analytic expressions for the change in the primitive variables across both a rarefaction and shock. We can then solve these to find the state in-between the left and right waves—the star state.

Shock jump conditions

For the case where the left or right wave is a shock, we use the Rankine-Hugoniot jump conditions to connect the states across the wave. The generalized version of the jump conditions for a system is:

\[\frac{\bf{F}({\bf U}_\star) - {\bf F}({\bf U_s})}{{\bf U}_\star - {\bf U}_s} = S\]

where \(s \in [L, R]\) is the state to the left or right of the interface and \(S\) is the shock speed.

We can write the jump conditions in the frame of the shock as (for the left wave). Then:

\[\begin{align*} \rho_L \hat{u}_L &= \rho_\star \hat{u}_\star \\ \rho_L \hat{u}_L^2 + p_L &= \rho_\star {\hat{u}_\star}^2 + p_\star \\ \rho_L e_L \hat{u}_L + p_L \hat{u}_L + \frac{1}{2} \rho_L \hat{u}_L^3 &= \rho_\star e_\star \hat{u}_\star + p_\star \hat{u}_\star + \frac{1}{2}\rho_\star {\hat{u}_\star}^3 \end{align*}\]

where \(\hat{u} = u - S\) (for both the \(\star\) and \(L\) velocity), and \(S\) is the shock speed.

With a lot of algebra, you can find the relation of \(u_\star\) to \(u_L\) as:

\[u_\star = u_L + \frac{2 c_L}{\sqrt{2 \gamma(\gamma-1)}} \frac{1 - \frac{p_\star}{p_L}}{\sqrt{1 + \frac{\gamma + 1}{\gamma -1} \frac{p_\star}{p_L}}}\]

and similarly for a shock across the right wave:

\[u_\star = u_R - \frac{2 c_R}{\sqrt{2 \gamma(\gamma-1)}} \frac{1 - \frac{p_\star}{p_R}}{\sqrt{1 + \frac{\gamma + 1}{\gamma -1} \frac{p_\star}{p_R}}}\]

Shock speed

Likewise, we can find the shock speed for the gamma-law case, via the mass flux condition across the shock, giving:

\[S = u_R + c_R \sqrt{\frac{\gamma + 1}{2\gamma} \left (\frac{p_\star}{p_R} \right ) + \frac{\gamma -1}{2\gamma}}\]

Rarefaction solution

To understand a rarefaction, let’s replace the pressure equation in our system with an entropy equation. Entropy evolves according to:

\[\frac{Ds}{Dt} = 0\]

but now we need to replace the pressure gradient in the momentum equation:

\[\frac{\partial p(\rho, s)}{\partial x} = \left . \frac{\partial p}{\partial s} \right |_\rho \frac{\partial s}{\partial x} + \left . \frac{\partial p}{\partial \rho} \right |_s \frac{\partial \rho}{\partial x} = \left . \frac{\partial p}{\partial s} \right |_\rho \frac{\partial s}{\partial x} + \frac{p\Gamma_1}{\rho} \frac{\partial \rho}{\partial x} \]

and our system becomes:

\[\begin{split} \left ( \begin{array}{c} \rho \\ u \\ s \end{array} \right )_t + \left ( \begin{array}{ccc} u & \rho & 0 \\ c^2/\rho & u & \frac{p_s}{\rho}\\ 0 & 0 & u \end{array} \right ) \left ( \begin{array}{c} \rho \\ u \\ s \end{array} \right )_x \end{split}\]

with \(p_s = \partial p / \partial s |_\rho\). This has the same eigenvalues as our primitive variable system, but now the right eigenvectors are:

\[\begin{split} {\bf r}^{(-)} = \left (\begin{array}{c} 1 \\ -c/\rho \\ 0 \end{array} \right ) \qquad {\bf r}^{(0)} = \left (\begin{array}{c} 1 \\ 0 \\ -c^2 / p_s \end{array} \right ) \qquad {\bf r}^{(+)} = \left (\begin{array}{c} 1 \\ c/\rho \\ 0 \end{array} \right ) \end{split}\]

We see that entropy is constant across a rarefaction. We can use this to find the solution linking the states across a rarefaction.

Note

We can only use this system when describing rarefactions. Shocks are dissipative, so entropy will increase across them.

We’ll work back with the primitive variables now. Across the left wave (’\(-\)’ ), the characteristic variable \(w^{(+)}\) is constant, which is defined as:

\[{\bf l}^{(+)} \cdot d{\bf q} = 0\]

Finding the left eigenvalue and doing the dot product gives:

\[du + \frac{dp}{\rho c} = 0\]

across the left wave. The general solution to this is:

\[u = - \int \frac{dp}{\rho c}\]

For a gamma-law equation of state, constant entropy means:

\[p = K \rho^\gamma\]

and we can do the integral and we find:

\[u + \frac{2c}{\gamma - 1} = \mbox{constant}\]

Similarly across the right wave we find:

\[u - \frac{2c}{\gamma - 1} = \mbox{constant}\]

These are called the Riemann invariants.

We can use these to link the states across the rarefaction, and we find:

\[u_\star = u_L + \frac{2 c_L}{\gamma - 1} \left [ 1 - \left ( \frac{p_\star}{p_L} \right )^{(\gamma-1)/2\gamma} \right ]\]

for the left rarefaction, and

\[u_\star = u_R - \frac{2 c_R}{\gamma - 1} \left [ 1 - \left ( \frac{p_\star}{p_R} \right )^{(\gamma-1)/2\gamma} \right ]\]

for the right rarefaction.

Implementation

import matplotlib.pyplot as plt
import numpy as np
from ppmpy import RiemannProblem, State

ppmpy provides a State class that holds the left or right interface state and the RiemannProblem class that implements the Riemann problem, with methods to find the star state and then find the state on the interface.

The find_star_state() method solves for the star state. This needs to find the \(p_\star\) such that:

\[u_{\star,L}(p_\star) = u_{\star,R}(p_\star)\]

If \(p_\star > p_s\), for \(s \in {L, R}\), then we are a shock (compression), otherwise we are a rarefaction. So our functions are:

\[\begin{split} u_{\star,L}(p_\star) = u_L + \left \{ \begin{array}{cc} \frac{2 c_L}{\sqrt{2 \gamma (\gamma -1)}} \frac{1 - {p_\star}/{p_L}}{\sqrt{1 + \frac{\gamma+1}{\gamma-1} \frac{p_\star}{p_L}} } & p_\star > p_L \\[4 mm] \frac{2 c_L}{\gamma -1} \left [ 1 - \left ( {p_\star}/{p_L} \right )^{(\gamma-1)/(2\gamma)} \right ] & p_\star \le p_L \end{array} \right . \end{split}\]

and

\[\begin{split} u_{\star,R}(p_\star) = u_R - \left \{ \begin{array}{cc} \frac{2 c_R}{\sqrt{2 \gamma (\gamma -1)}} \frac{1 - {p_\star}/{p_R}}{\sqrt{1 + \frac{\gamma+1}{\gamma-1} \frac{p_\star}{p_R}} } & p_\star > p_R \\[4 mm] \frac{2 c_R}{\gamma -1} \left [ 1 - \left ( {p_\star}/{p_R} \right )^{(\gamma-1)/(2\gamma)} \right ] & p_\star \le p_R \end{array} \right . \end{split}\]

We solve this by picking a guess for \(p_\star\) and then root finding on the constraint that the velocity in the star region is the same when we come from the left as when we come from the right.

Let’s consider the Sod problem. We can visualize the solution in the \(u\)-\(p\) plane via the plot_hugoniot() method.

from ppmpy.riemann_exact import plot_hugoniot

left = State(p=1.0, u=0.0, rho=1.0)
right = State(p=0.1, u=0.0, rho=0.125)

rp = RiemannProblem(left, right)
rp.find_star_state()

fig = plot_hugoniot(rp)

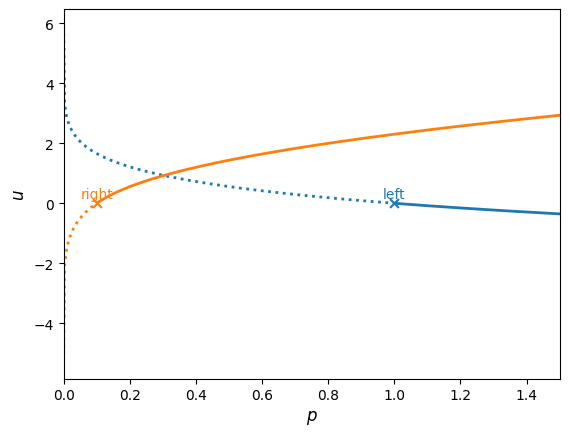
In this figure, a shock is shown as a solid line and a rarefaction is shown as a dotted line. The solution is where the curves intersect, and we see that the a shock connects the right state to the star state and a rarefaction connects the left state to the star state.

Sampling the Solution

To find the interface state, we need to sample the solution. This is done via the sample_solution() method.

Consider the following 4 cases:

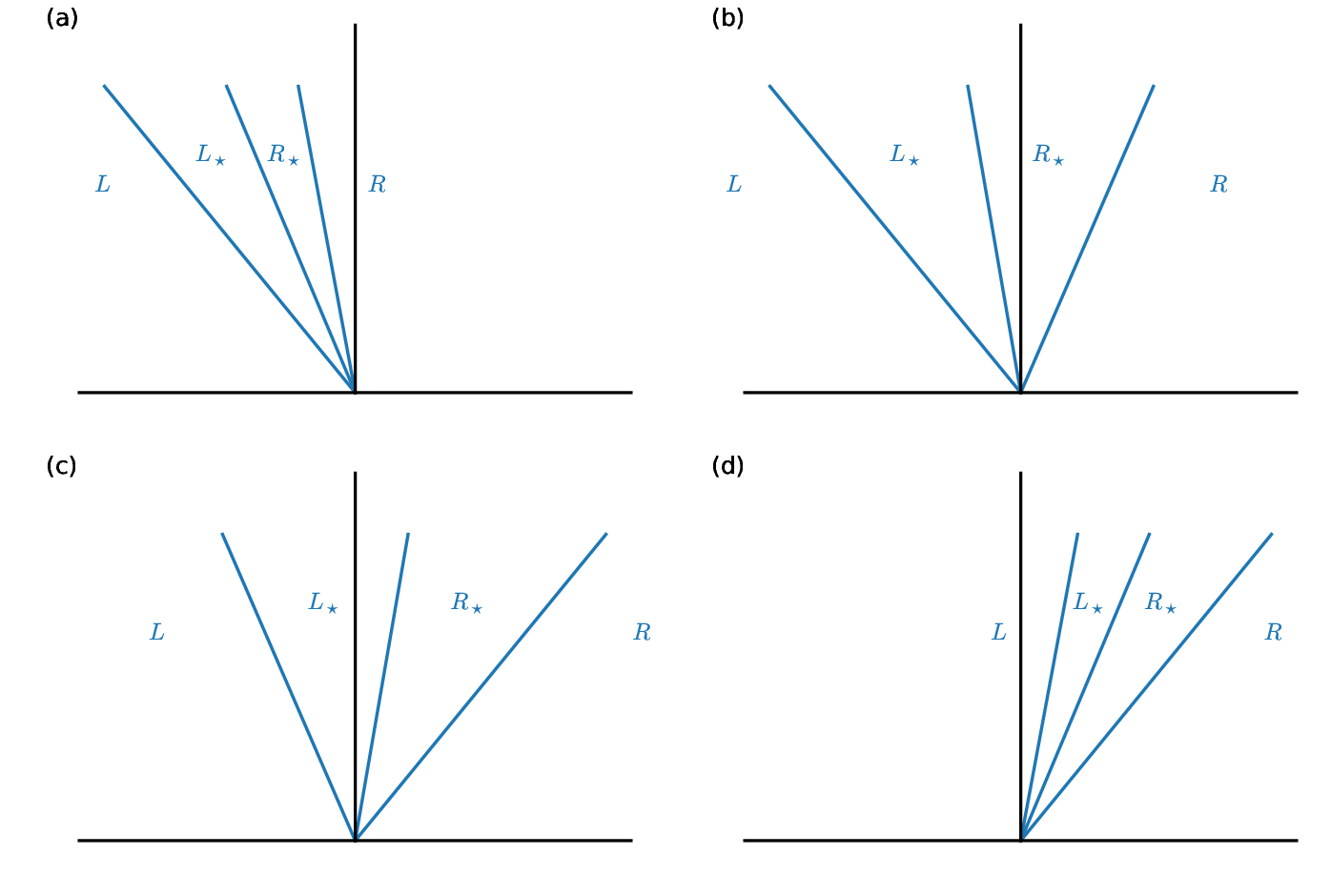
Cases (a) and (d) represent supersonic flow to the left or right—all 3 waves are on one side of the interface.

• For case (a), all 3 waves are to the left of the interface, so state \(R\) is on the interface.

• For case (d) is similar, all 3 waves are to the right of the interface, so state \(L\) is on the interface.

In cases (b) and (c), one the “\(+\)” and “\(-\)” waves are on either side of the interface and the only difference is the center (”\(0\)”) wave, or contact discontinuity. So we would determine which of the star states is on the interface based on the sign of the contact discontinuity’s speed.

• For case (b), the contact is moving to the left so \(R_\star\) state is on the interface

• For case (c), the contact is moving to the right, so the \(L_\star\) state is on the interface.

Wave speeds

Shock case

For a shock, the speed of the shock comes from the Rankine-Hugoniot conditions.

For the left wave, the shock speed is:

\[ S = u_L - c_L \sqrt{\frac{\gamma + 1}{2\gamma} \left (\frac{p_\star}{p_L} \right ) + \frac{\gamma -1}{2\gamma}} \]

For the right wave, it is:

\[ S = u_R + c_R \sqrt{\frac{\gamma + 1}{2\gamma} \left (\frac{p_\star}{p_R} \right ) + \frac{\gamma -1}{2\gamma}} \]

Contact discontinuity

A contact discontinuity propagates in the star region, and the velocity there is \(u_\star\) and is constant in that region, so the contact just propagates at this speed:

\[S_0 = u_\star\]

Rarefaction

A rarefaction is subsonic, but it is spread out (it is not a discontinuity). We call the leading part the “head” and the trailing part the “tail”. The head and tail move at different speeds, just \(u \pm c\) corresponding to the region they abut.

For a left rarefaction:

\[S_\mathrm{head} = u_L - c_L\]

\[S_\mathrm{tail} = u_\star - c_\star\]

For a right rarefaction:

\[S_\mathrm{head} = u_R + c_R\]

\[S_\mathrm{tail} = u_\star + c_\star\]

Note that \(|S_\mathrm{head}| > |S_\mathrm{tail}|\), so the rarefaction spreads out over time.

Also, it is possible for the rarefaction to span the interface—with the head on one side and the tail on the other. We’ll deal with this shortly.

Density

To compute the rarefaction speed, we need to know the density in the star state (so we can evaluate \(c_\star\)). We will need this anyway for either a shock or a rarefaction to compute the final fluxes if a star state is on the interface.

For a rarefaction, since entropy is constant, we have:

\[\frac{p_s}{\rho_s^\gamma} = \frac{p_\star}{\rho_{\star,s}^\gamma}\]

where \(s \in {L, R}\) is the state outside of the star region.

For a shock, the jump conditions tell us the density:

\[\rho_{\star,s} = {\rho_s} \frac{\frac{p_\star}{p_s} + \frac{\gamma-1}{\gamma+1}}{\frac{p_\star}{p_s}\frac{\gamma-1}{\gamma+1} + 1}\]

Sampling

The sampling procedure is the following:

• Look at the sign of the contact speed, \(S_0\):

  • If \(S_0 > 0\) then we are either in the \(L\) or \(L_\star\) state

    • Look at the speed of the left shock or rarefaction to determine if we are in the \(L\) or \(L_\star\) state

  • If \(S_0 < 0\) then we are either in the \(R\) or \(R_\star\) state

    • Look at the speed of the right shock or rarefaction to determine if we are in the \(R\) or \(R_\star\) state

The one catch is when the rarefaction spans the interface, e.g., \(S_\mathrm{head} < 0 < S_\mathrm{tail}\) for a left rarefaction.

In this case, we would use the Riemann invariant to find the state at the location of the interface inside the structure of the rarefaction.

qint = rp.sample_solution()
print(qint)

rho: 0.4263194281784952; u: 0.9274526200489498; p: 0.30313017805064685

This state can then be used to compute the fluxes through the interface:

\[\begin{split}F_{i+1/2} = \left ( \begin{array}{c} \rho_{i+1/2} u_{i+1/2} \\ \rho_{i+1/2} (u_{i+1/2})^2 + p_{i+1/2} \\ u_{i+1/2} p_{i+1/2} / (\gamma - 1) + \frac{1}{2} \rho_{i+1/2} (u_{i+1/2})^3 + u_{i+1/2} p_{i+1/2} \end{array} \right )\end{split}\]