Using the Euler solver

Using the Euler solver#

ppmpy provides an Euler class that solves the Euler equations using PPM.

import numpy as np
import matplotlib.pyplot as plt

from ppmpy import Euler

Sod problem#

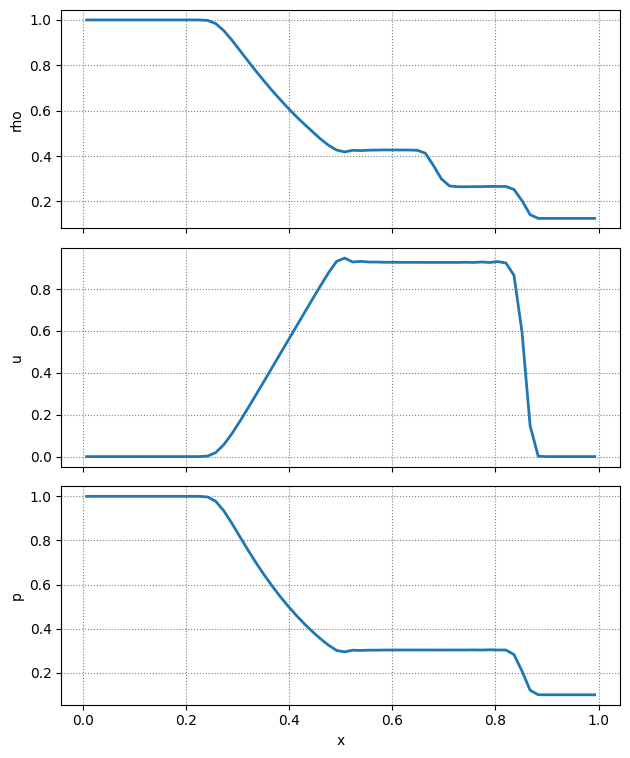
Here we do an example of the Euler solver running the standard Sod problem. The initial conditions for this are provided by the ppmpy.initial_conditions module.

from ppmpy.initial_conditions import sod

We setup the Euler solver by telling it the number of zones, CFL number, and the initial condition function to use.

nx = 64
C = 0.5
e = Euler(nx, C, init_cond=sod)

We can then evolve–here we evolve for 0.2 s. We set verbose=False to suppress the output of the timestepping.

e.evolve(0.2, verbose=False)

Finally a plot.

fig = e.plot_prim()
_images/3c1066b9308b4610d0a581afe0c5058215ede4b35174356ec39b99c2c9345270.png

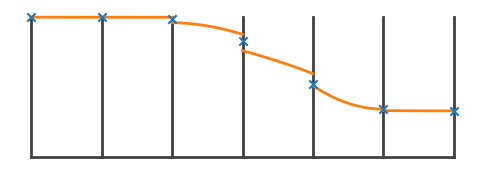
We can also visualize the parabolia reconstruction. Here’s the pressure near the shock.

gp = e.grid.draw(lo_index=55, hi_index=60, stretch=2)
e.draw_prim(gp, e.v.qp)
_images/a76c0460689849860f5b4b41f53c021f1b449ebe6a7905a43472115bc0bff4b5.png

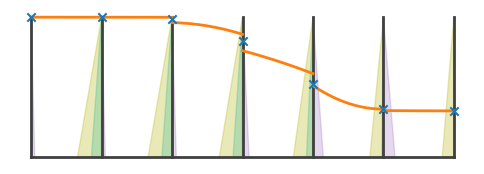
We can also show to which interface each of the 3 characteristic waves moved in each cell by drawing their domain of dependence.

e.draw_waves(gp)
gp.fig
_images/fdc903897b309af01a3b9a34a37fdc513f90e72f6b5e43ec9f01d1e3751efd57.png

Custom initial conditions#

Let’s setup our own initial conditions for a general shock tube. We will want to be able to pass parameters to the initial condition function to set the left and right state–this is accomplished by setting the params keyword argument in the Euler class to a dictionary with the parameters.

The ratio of specific heats, \(\gamma\), is provided in params as well. If not explicitly set when params is passed it, and default value of \(1.4\) will be used.

Here’s our new initial conditions:

def shock_tube(euler):

    gamma = euler.params["gamma"]
    
    rho_l = euler.params["rho_l"]
    u_l = euler.params["u_l"]
    p_l = euler.params["p_l"]
    rho_r = euler.params["rho_r"]
    u_r = euler.params["u_r"]
    p_r = euler.params["p_r"]

    idx_l = euler.grid.x < 0.5
    idx_r = euler.grid.x >= 0.5

    euler.U[idx_l, euler.v.urho] = rho_l
    euler.U[idx_l, euler.v.umx] = rho_l * u_l
    euler.U[idx_l, euler.v.uener] = p_l/(gamma - 1.0) + 0.5 * rho_l * u_l**2

    euler.U[idx_r, euler.v.urho] = rho_r
    euler.U[idx_r, euler.v.umx] = rho_r * u_r
    euler.U[idx_r, euler.v.uener] = p_r/(gamma - 1.0) + 0.5 * rho_r * u_r**2

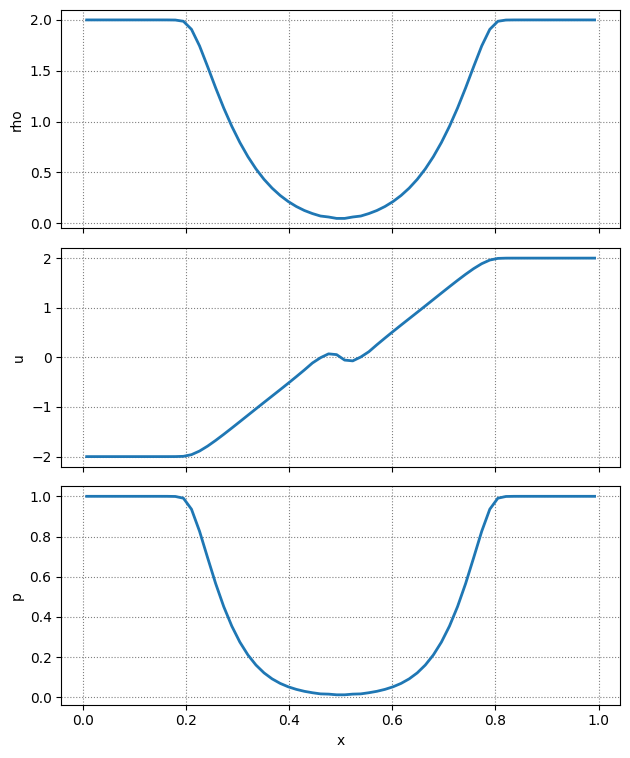
Let’s do a double rarefaction / vacuum problem

params = {"rho_l": 2.0, "u_l": -2.0, "p_l": 1.0,
          "rho_r": 2.0, "u_r": 2.0, "p_r": 1.0}
e = Euler(nx, C, init_cond=shock_tube, params=params)
e.evolve(0.1, verbose=False)

fig = e.plot_prim()
_images/6c8d35ec625e079c0fe20de6d79a1cd951d75baf963f24189c9b0b8a2e2b93e0.png
Contents